In part 1 of this blog post I provided some reasons as to why transfer is difficult, particularly in mathematics. The use of concrete materials as well as of highly contextualized tasks may increase the probability of short-term comprehension but hinder learning in the future.
REASONS
- “Any extraneous detail in the presentation of information tends to distract learners from the relevant content, leading to poorer recall for that material. “ *see the “seductive details effect” (Garner et al., 1989; Harp and Mayer, 1998; De Loache 1991, 1995; DeLoache and Burns, 1994; Son and Goldstone, 2009)
That can happen if the way you introduce a concept or practice a skill is overly “engaging” (I can think of many examples, starting with “food math” – pizza fractions, gummy bears counting etc., and ending with “pretty” worksheets).
- “More insidiously, even those concrete details that are integral and relevant to the examples may harm learning by impairing transfer to new situations.” (Clement et al., 1994; Goldstone and Sakamoto, 2003; Kaminski et al., 2008).
This means that the features that may have enabled students to perform an initial task made it difficult for them to transfer the learning to an analogous situation in which the surface details were changed, and to perceive the connection between the two contexts.
This leaves us with an apparent paradox: the very qualities that enable knowledge acquisition (concreteness, familiarity, personal relevance) are detrimental to knowledge transfer and generalization.
………………………………………………………………………………………………………………..
SOLUTIONS
In the research literature (see references at the end) and education reports (from TIMSS, PISA etc.) that I read a few strategies were consistently mentioned. To me they look like good teaching because you cannot really divorce transfer of learning from acquisition of knowledge and skills. However, as in the examples above, teachers may occasionally use inadequate methods in order to maintain student motivation, and being aware of them is important. All of these strategies are known to teachers but maybe their preponderance in teaching is lower.
|
All subjects |
Math-specific |
| Presentation of multiple cases | Shuffling of math problems |
| Compare and contrast | Multiple solutions or approaches |
| Features matrix | Embedded problem-solving |
| Example vs. Non-Example | Liminal Variation |
| Generalization | Fewer “real-math” problems |
| “Faded” concreteness | More complex problems |
| Analogies | Fewer math topics, more depth |
1. Presentation of multiple cases
Multiple cases presentation enables students to retain specific features within a broader context and it is a step towards generalization.
To give you a simple example (that I tweeted last week) the highly contextualized presentation of a parallelogram that my students had been previously exposed to made it difficult for them to recognize parallelograms in other contexts (different length side, different position etc.)
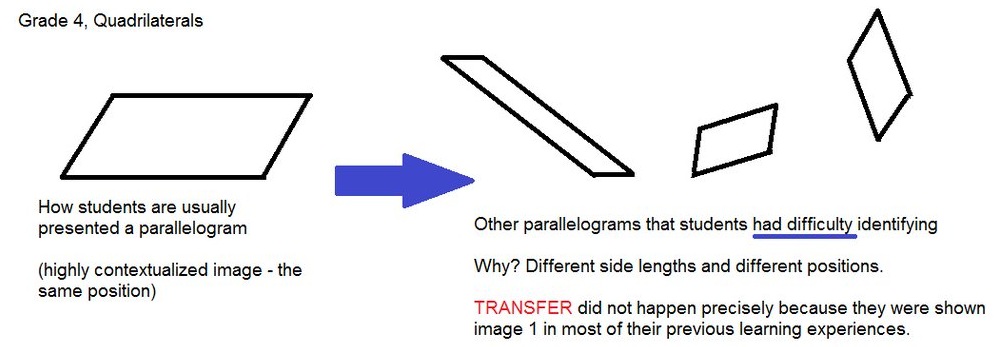
Think about your own domain (it may be biology, physics or even language) and plan for this variety. As teachers we may take it for granted but the very example above proves that children do think differently.
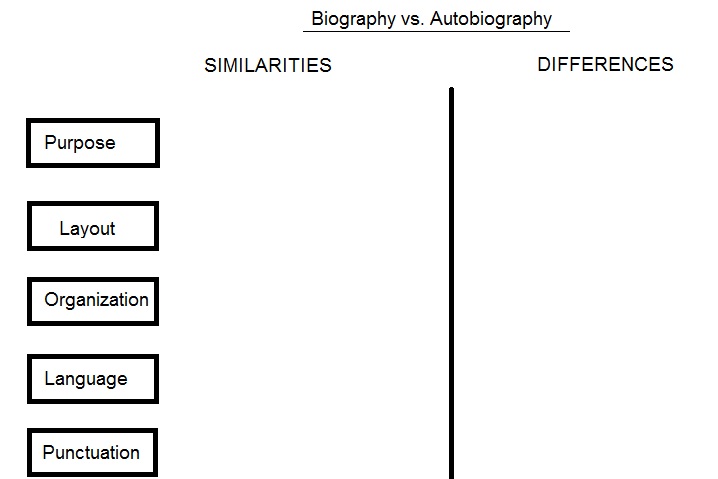
2.Compare and contrast
Noticing the similarities and the differences between two objects (shapes, fractions, words, science terms etc.) is critical in both preventing misconceptions (e.g. 0.9 vs. 0.09) and in better transfer in the future.
Research showed that even if strategy 1 (multiple cases) is used, only students who were involved in subsequent activities of comparing /contrasting managed to transfer the new information. *(See Gickand Holyoak, 1983; Catrambone and Holyoak, 1989; Cummins, 1992; Loewensteinetal, 2003; Gentneretal., 2009; Christieand Gentner, 2010; Richland and McDonough, 2010)
“Appropriately arranged contrasts can help people notice new features that previously escaped their attention and learn which features are relevant or irrelevant to a particular concept .”(Bransford et al., 2000)
*See example for writing below. Think of your own subject – What are very similar (concepts, terms, items etc.) that your students are very likely to have difficulty discriminating?
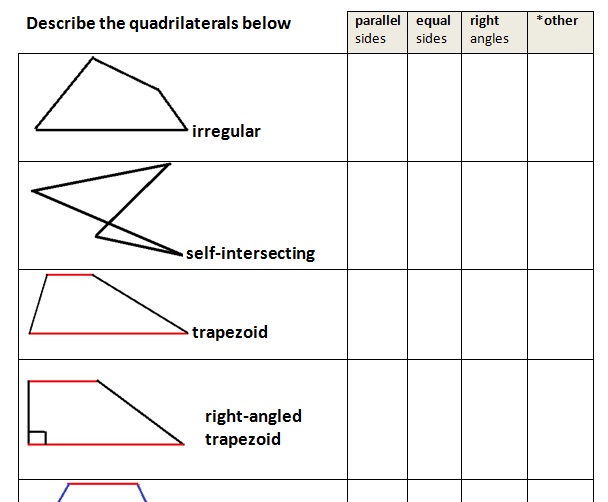
3.Features matrix
It is usually used when more than two items bear similar features.
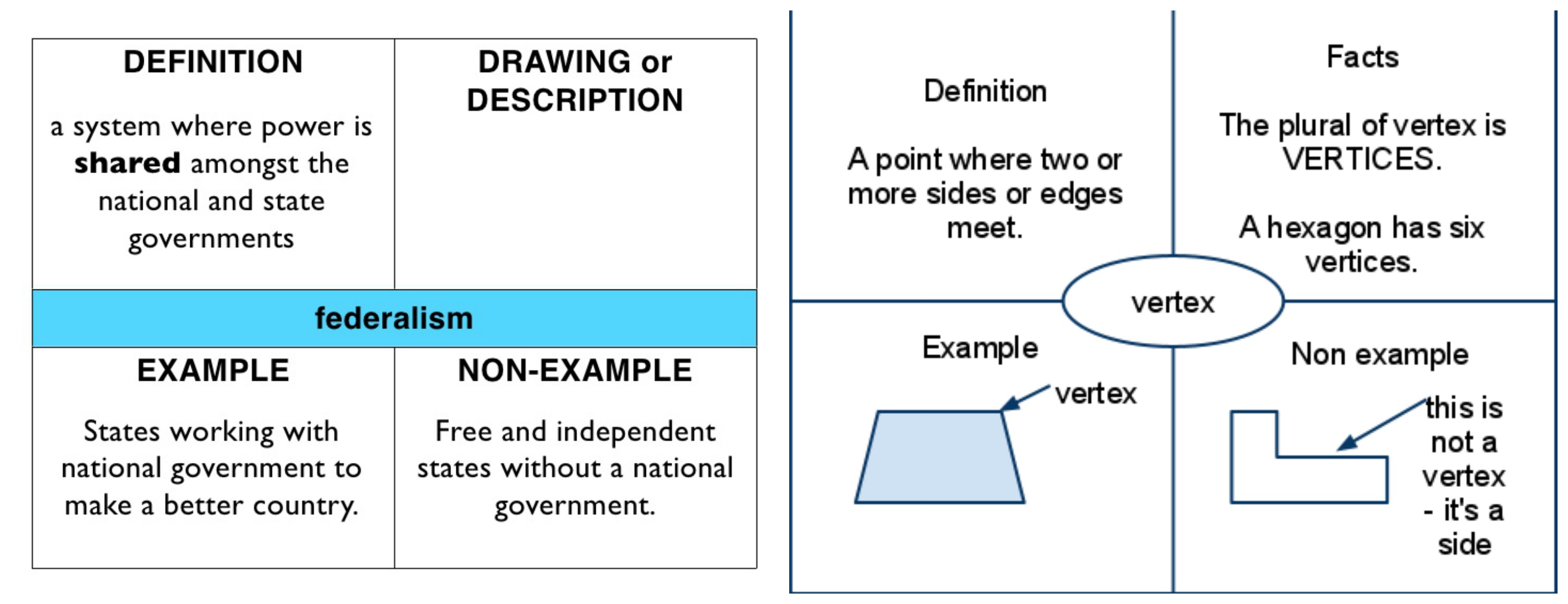
4.Example vs. Non-Example
Again, this helps students to discriminate similar items and consolidate their understanding so that they can apply learning in the future.
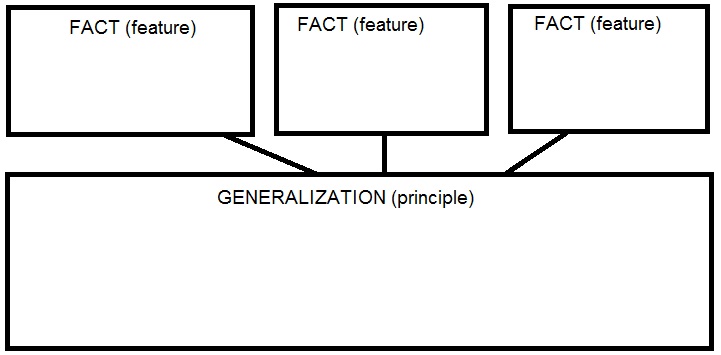
5.Generalization
This is a critical step from analysis to synthesis and it can take many forms (it can be done with the whole class after students have been manipulating more concrete materials or were involved in somewhat contextualized tasks).
6.”Faded” concreteness
Teachers need to adopt the “faded” concreteness strategy so that students can dissociate the principles from the initial concrete and highly contextualized experience. Systematic exposure to increasingly idealized models is essential. *(See Kotovsky and Gentner, 1996; Scheiter et al., 2010; Fyfeetal., 2014).
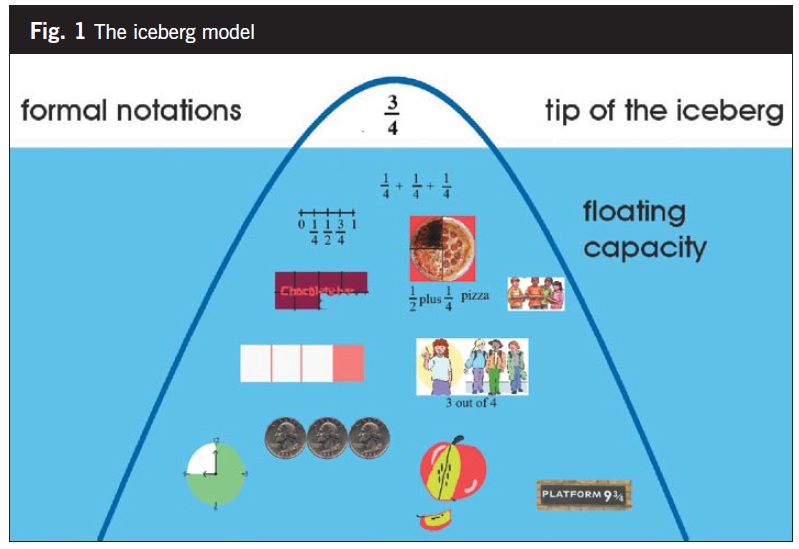
*Above is the “iceberg model” provided by the researchers at the Freudenthal Institute for Science and Mathematics, to support teacher thinking about the sequential processes involved from pre-formal, informal, and formal stages.
Another example below:
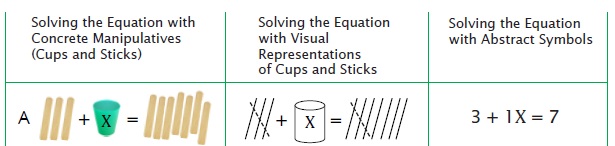
7. Analogies
Effective analogies enable students to develop their abstraction schema and to further develop strategies to recognize critical features and make connections in the future, all of which enable better transfer of learning. *(See Learning and Transfer: A General Role for Analogical Encoding, Gentner Dedre et al., Journal of Educational Psychology, 2003)
It is important that analogies are planned carefully so that students would not confuse the analogy with the target, and more time needs to be spent on finding both similarities and differences between them. (*See more reference at the end of the post)
Specific MATHEMATICAL strategies
- Shuffling of math problems
In block practice the effect of overlearning was noticed consistently (students learn a type of problem and apply the strategy in many similar math problems). Not only it does not improve mathematics performance but it can impede student understanding of bigger concepts which are shared by very different math problems (isomorphism). This effect is due to block practice. (*See The Shuffling of Mathematics Problems Improves
Learning, Doug Rohrer & Kelli Taylor, 2007)
“If a practice set includes a randomly arranged variety of problem types, students learn to pair each kind of problem with the appropriate procedure. In other words, a mixed practice schedule requires that students learn not only how to perform each procedure but also which procedure is appropriate for each kind of problem.” (*See Kester, Kirschner, & Van Merrienboer, 2004).
*For classroom examples and more research see my post Where Direct Instruction Fails .
2. Multiple solutions or approaches
In Japanese classrooms, flexible approaches are consistently encouraged and often a lesson is centered around a single math problem.
“This is made clear by the way the question is framed and the teachers must ask their students to ‘think about as many different solutions as possible‘.” (David Burghes & Derek Robinson, Enhancing Mathematics Teaching and Learning, 2009)
3. Embedded problem-solving
“Problem solving is embedded in Singapore texts, not as a separate activity but as central to every skill and concept discussion.” (*See Ginsburg, Alan et al., What the United States Can Learn From Singapore’s World-Class Mathematics System, American Institute for Research)
4. Liminal Variation
The textbooks in the UK and the US use repetition of problems consistently, yet they often fail to enable students to generalize and transfer learning. *(Yeap, Ferrucci & Carter, 2006; Vincent & Stacey, 2008)
Compare with the Chinese textbooks and teaching:
“By systematically keeping some things invariant while others are varied and then changing what is varied and what remain invariant, students are able to “see” (to directly perceive or intuit) concept(s).” (Teaching with Procedural Variation: A Chinese Way of Promoting Deep Understanding of Mathematics, Mun Yee Lai & Murrai Sara, International Journal for Mathematics Teaching & Learning, 2012)
“Variation theory is posited on the view that when certain aspects of a phenomenon vary while its other aspects are kept constant, those aspects that vary are discerned. In other words, learning amounts to being able to discern certain aspects of the phenomenon that one previously did not focus on or which one took for granted, and simultaneously bring them into one’s focal awareness”. (Lo, Chik & Pang, 2006).
According to Gu et al. (2004), procedural variation is derived from three forms of
problem solving:
(1) varying a problem: extending the original problem by varying the conditions, changing the results and generalization;
(2) multiple methods of solving a problem by varying the different processes of solving a problem and associating different methods of solving a problem;
(3) multiple applications of a method by applying the same method to a group of similar problems.
The principles below are not strategies but observations from various reads.
- Fewer “real-math” problems
Similarly to the concrete or highly contextual tasks, real-math tasks may increase student engagement but they can also diminish the attention to critical features, connections or structure underlying the problem.
(Just think about using real coins in a class of 20 students so that they can practice their addition and subtraction- much attention will be diverted to coins that roll or fall, to who has more or fewer, to the dynamics between the children etc.)
- More complex problems
In Asian education systems solving complex problems takes 39% of class time compared to the US, for instance, where only 6% of the time is devoted to similar problems. (TIMMS )
This is in the same line with many findings in general literature:
“Learning and instruction that is based on fragmentation of complex tasks into sets of distinct elements without taking their interaction into account fails because learners ultimately cannot integrate and coordinate the separate elements in transfer situations.” (A New Approach to Instructional Design; cited papers by Wightman & Lintern, 1985; Clark & Estes, 1999; Perkins & Grotzer, 1997; Spector & Anderson, 2000)
“The methods that work for reaching isolated, specific objectives are not the best for reaching integrated objectives and transfer of learning.” (Merrienboer & Crook, 1997)
- Less is more
Comparing the US with Singapore, for instance, the differences were staggering:
“The median coverage in the US was 70% more math topics than in Singapore. Florida had 160% more coverage per grade than in Singapore. With so many more topics per grade, U.S. standards are not able to expose students to the same depth of content as Singapore standards.” (American Institute for Research Report, 2009)
………………………………………………………………………………………………………………….
Other references:
- TIMSS, International Data Bases , 2003 and 2007
- PISA, OECD iLibrary
- Transfer of Learning: Issues and Research Agenda, National Research Foundation, 2002
- Alternative Perspectives on the Transfer of Learning: History, Issues, and Challenges for Future Research, The Journal of Learning Sciences, 2006
- The Cognitive Costs of Context: The Effects of Concreteness and Immersiveness in Instructional Examples, Samuel D. Bay et al, 2015