Where Direct Instruction Fails: Willingham, Memorization, and Conceptual Understanding (2)

In my previous post I wrote about the overemphasis on memorization and drills and brought some arguments for balancing all three aspects of knowledge in mathematics: factual, procedural, and conceptual. Let’s review:

1. Memorization of math facts is important. It allows for complex tasks to be carried out.
2. Procedures should be taught after or in tandem with concepts. One supports the comprehension of the other.
3. Block practice (in textbooks and in teaching) is detrimental to learning. The overlearning as well as familiarity effects occur.
4. Excessive modeling and examples in math can actually interfere with learning. They increase performance in the short term but hinder learning in the long run.
5. Space out practice and interleave mathematical concepts. If you focus on a topic (i.e. fractions) make sure your students not only apply it in different contexts, but are also engaged in solving problems you previously taught (i.e. geometry or measurement topics). Even better, use fractions, measurement, and geometry together (Example: 1/3 of the area of a rectangle is red. Knowing that the perimeter is 64m and one of the sides is 1,000cm, find out what part of the rectangle is red. – Knowledge of area and perimeter, knowledge of fractions, and knowledge of measurement conversion).

Now, as promised, I will exemplify from my own teaching practice how conceptual understanding is built.

Let’s assume you are to be taught area and perimeter.

PERIMETER

In a direct instruction approach, you would be given the formulas and generally asked to solve a multitude of problems applying them (that is how I was taught).

Perimeter = sum of all sides in a polygon

So you keep solving problems ad nauseam. Nothing important neither about area nor about its relationship with the perimeter is learned. What you actually practice is addition (and/or multiplication).

Through inquiry, not only did I encourage students to ask and answer conceptual questions (Form – What is perimeter?, Function – How does it work? How is it calculated?, Change – How does it change? etc.), but consistently monitored their understanding through more questions.

Open-ended tasks and questions are ideal for that ( I wrote about them here and here).

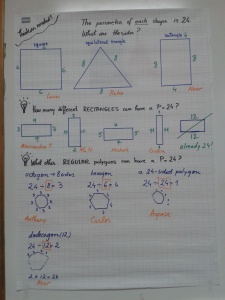
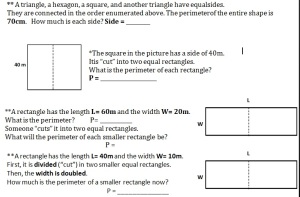
• “The perimeter of these shapes is 24. What are their sides?”

Now compare that above with what direct instruction would mean: “Find out the perimeter of a rectangle where the length is 8 and the width is 4.” Definitely less cognitive work than working out different shapes AND sides with the same perimeter. So yes, “memory is the residue of thought” – thinking through inquiry IS hard work.

• Extending the understanding: “How many rectangles can we make with the same perimeter?”

• Extending even further: “How many polygons can we make with the same perimeter?”

Now, we have irregular and even self-intersecting polygons. Nice, I think, for 4^th grade math in second language.

What did the students notice? Number patterns. 24 is now seen as a relationship between factors (1,2,3, 4, 6, 8…).

Something else? Sides relationship when having the same perimeter. When one side increases (say length) the other decreases (width).

What else? Perimeter conservation even when the shape is changed (24 is still 24 even whether it is a triangle or a square).

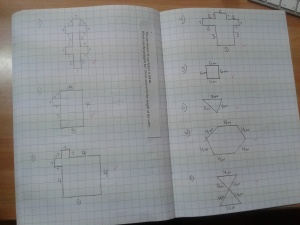
Practice was also done in various contexts:

• grids
• paths
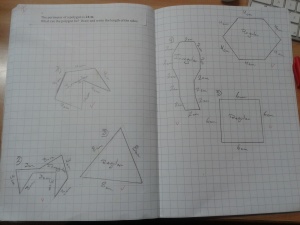
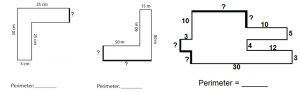
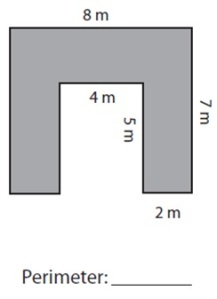
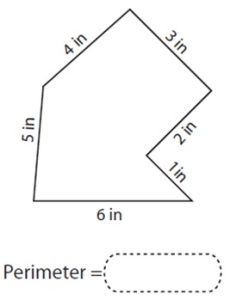
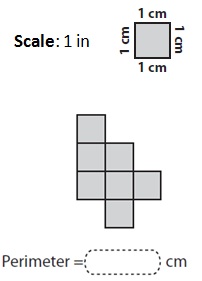
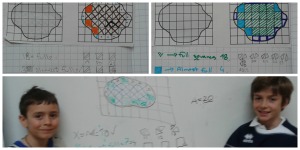
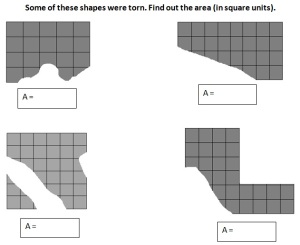
• known perimeter but unknown sides
• known sides but unknown perimeter etc. (see the photos – some samples of tasks)

AREA

Again, in direct instruction the formula is provided (Area= length x width), and countless problems follow – usually, after having been modeled by the teacher. Block practice again, and not much understanding – just computation with little relevance.

In inquiry, we started with questions.

• What is area? How can you find it out?
• Why do we have to multiply? Why can’t we use a different math operation?
• Where does the, say, cm² come from? Why is that little “2” there? (This led to a discussion and discrimination between Perimeter – uni-dimensional, length, hence measured just, say, in cm, Area – 2-dimensional, length and width, hence the cm x cm = cm², and Volume – 3-dimensional, length X width X depth, hence  cm x cm x cm= cm³⁾
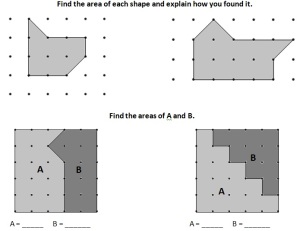
• Why don’t we multiply all sides, like we added all the sides in the perimeter? (A student asked this question and I find it relevant. As experts, we no longer grasp the difficulty of understanding for children. Then another student explained…as you can see in the photo).
• Take 6 tiles. Move them around and create combinations. Does the area change? What about the perimeter?
• If I have the same area, does the perimeter change?
• If I have the same perimeter, does the area change?
• If you cut out a shape do you: a) reduce its area?, or b) reduce its perimeter? Investigate further and try to find a pattern, a generalization or an explanation.
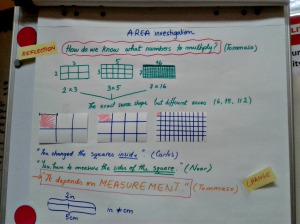
• How do we know what numbers to multiply? (question from another kid, a quite relevant one) What if I have 3 rectangles with the exact same perimeter and sides (see the equal papers I attached)? Why can I have 2 x3 = 6 in the first but 3 x 4 = 12 in the second given that the rectangles are exactly the same? With the help of his peers, he understood
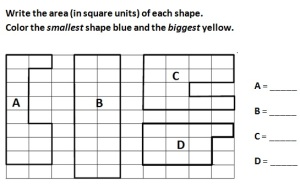
• How can we find out area in irregular shapes? Can we be accurate or do we just estimate?
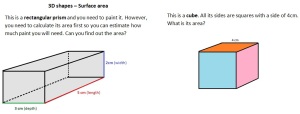
• How can we find out surface area in 3-d shapes? What is important to know and do?

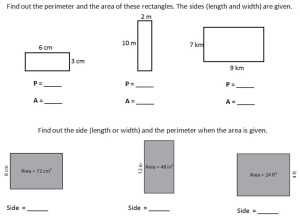
Aside from questioning, students practiced many types of problems  (some below).

All of these questions led to an in-depth understanding of BOTH concepts, area and perimeter, and of the RELATIONSHIP between them. Moreover, several OTHER CONNECTIONS were made – with measurement, patterns, doubling/halving, with squared numbers (area in squares), concepts related to 3-D shapes (vertices, faces), to position and grids etc.

It was a pure coincidence that today I came across these videos and post by Robert Kaplinsky through David Wees. If you think conceptual understanding does not matter, think again. These are 8^th graders asked to show understanding of the concept of perimeter. If you think these are isolated cases, you are wrong. Read his entire post on depth of knowledge – it is illuminating.

As Robert Kaplinsky writes:
Procedural fluency? CHECK.
Conceptual understanding? CHECK.
But then….

Procedural fluency? NO.
Conceptual understanding? NO.

Why this insistence on conceptual understanding and making connections? Because all reports, whether from TIMSS or other organizations, point to their importance.

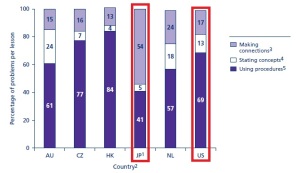
• Comparing Japan and Hong Kong with other 31 countries, TIMSS 1999 report highlighted how differently these countries approach mathematics in their classes. Out of the 4 types of problems encountered (repetition, mathematically related, thematically related, and unrelated), “Japanese mathematics lessons contained a higher percentage of problems per lesson that were mathematically related” while in the rest (including the U.S. and the U.K.) they were repetition-based (65%).
• The same report finds that, for instance, in the U.S. students almost never have the opportunity to discuss the concepts and relationships involved in the problems they solve.

• Mathematically rich problems deepen student understanding. Reducing complexity is not the best way to engage students in better math. In direct instruction, complexity is reduced usually in two ways: explicit modeling and step-by-step procedures.

• Moreover, making connections is given far more emphasis (54%) than, say, in the U.S. (15%).

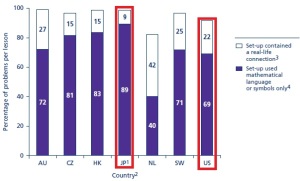
• In addition to this, relating mathematics to real-life is not conducive to understanding deep-level math. Again, the percentage variation between Japan (use of real-life connections is just 9%) and the U.S. (22%) is big enough to bust this myth.

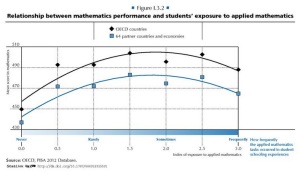
This is not surprising as PISA findings have also pointed out that after a while, real-life problems (applied mathematics) correlate negatively with performance. The same finding was discussed in The Handbook of Research on the Psychology of Mathematics Education, 2006 (more on these here ).

• On a similar note, excess use of manipulatives can hinder learning. While they are necessary in the first stages of building understanding, their overuse is associated with greater difficulty in building conceptual knowledge – students rely on them too often and can’t extend their thinking beyond these concrete materials. That is especially true when they have to make the leap to algebra, where purely mental objects are manipulated (Skemp, Psychology of Mathematics). Concepts become more complex and harder to generate (you can divide a shape in two, but it is harder to think of any number x divided by 2) – aspect also mentioned by Willingham or in other studies.

• Also, engage students in solving non-routine and inverse problems regularly (inverse problems – those that require the inverse of addition or multiplication, namely those that require knowledge of subtraction, division, identifying roots or factorizing):

“Inverse problems are more demanding, and cannot be reduced to deterministic methods. So they give rise to low scores, and they do so in a way that is hard to predict. This makes them distinctly awkward for those who devise test items within a target-driven and test-driven culture, where the assessors may be contractually obliged to return predictable results, and to avoid low scores. Hence, if such problems are set at all, they are usually adapted in some way to make pupil performance `more predictable’ (for example, by breaking down the unpredictable inverse problem into a more manageable sequence of steps – each of which is essentially a routine direct task). Teachers need to recognize the importance of such problems for pupils’ subsequent progress, and then devote sufficient time to them for pupils to achieve a degree of mastery.”

• Acceleration in math is not the best idea. Secondary mathematics teachers advise against it and suggest,

“(…) each topic can be treated on many levels, and those who grasp a basic concept should be faced with more challenging variations of the same material before they move ahead.”

It is preferable to extend this understanding and engage students in making deeper connections than to ask them to learn new concepts.

They also suggest “resisting the idea of breaking down every single problem in small, manageable steps, and encouraging the use of forward-looking methods.”

“Pressure to ‘achieve’ in the short-term often encourages pupils to become dependent on (and teachers to allow) `backward-looking’ methods that may seem to deliver answers in easy cases, but which sooner or later become an obstacle to progress.

Hence any internal scheme of work needs to make a clear distinction between:

(a) backward-looking methods that get answers in the short-term, but which trap pupils in old ways of working (as with finger counting, or idiosyncratic calculation methods, or reducing multiplication to repeated addition, or modeling questions about fractions in terms of pizzas – all of which may have transitional value, but which are known to block later progress if they become too strongly embedded),

(b) forward-looking methods, that may seem unnecessary if the perceived goal is merely to get answers to simple problems at a given stage, but which are important because of the way they reflect the inner structure of elementary mathematics, and are often essential for progress at the next stage.”

To conclude, drilling to ensure factual and procedural knowledge is not enough. In addition to 5 ideas I presented at the beginning remember to:

1. Make sure the mathematical problems you present to students are conceptually rich. Do not drill and focus on computation or procedures alone – in the long run, it will be their loss.
2. Make room for student questions: they give you an insight into both their understanding and misunderstandings. Covering content is irrelevant if your students didn’t grasp the concepts behind the procedures and facts you teach. You might be happy with their test scores, but next year’s teacher might become your favorite enemy. S/he has to reteach what you thought you were doing right.
3. Try to have in your lessons problems and tasks that are mathematically related. This deepens not only understanding of the individual concepts you teach but it also gives students the “big picture” of mathematics.
4. Real-life problems should be minimized. If you engage students in good math investigations, they will find them interesting and will enjoy solving them. “Real-life”tasks can often lead to distraction and are not particularly useful in further developing thinking.
5. Use manipulatives with care – it can become a sort of learned helplessness. If students in other countries can do without much of their use, everyone can. And it is not that they are helpful up to a point – but they become an impediment as the training wheels.
6. Use non-routine problems regularly and forward-looking methods. Resist the urge to help your students too much and scaffold with attention to their real needs. Children are capable of great understanding and your effort in helping them might actually be counterproductive.